知识点: 为了从数据中学习模型并对其进行推理，我们需要 be able to do inference. Pyro 包含 pyro.do，这是 Pearl 的 do-operator 的实现，用于因果推断。

Pyro 推断简介¶

现代机器学习的许多内容可以理解成近似推断并且使用 Pyro 这样的语言表达出来。为了说明这一点，让我们为一个简单的物理问题建立一个生成模型，并且使用 Pyro 的推理机制来解决它。

[1]:

import matplotlib.pyplot as plt
import numpy as np
import torch

import pyro
import pyro.infer
import pyro.optim
import pyro.distributions as dist

pyro.set_rng_seed(101)

假设我们试图得到某物的重量，但是我们使用的秤是不可靠的，并且每当我们称量同一物体时会给出稍微变动的读数。我们用以下概率模型来模拟：

\[{\sf weight} \, \sim \cal {\sf Normal}({\mu}, 1)\]

\[{\sf measurement} \, | {\sf weight} \sim {\sf Normal}({\sf weight}, 0.75)\]

其中，第一个式子表示该物体重量的先验分布，第二个式子表示对其进行测量的结果。该模型对应于以下随机函数：

[3]:

def scale(mu):
    weight = pyro.sample("weight", dist.Normal(mu, 1.0))
    return pyro.sample("measurement", dist.Normal(weight, 0.75))

[14]:

# Hint for the next section
def scale_obs(mu):
    weight = pyro.sample("weight", dist.Normal(mu, 1.))
    return pyro.sample("measurement", dist.Normal(weight, 0.75), obs=9.5)

随机函数的条件化¶

概率编程的真正威力是：把生成模型对观测数据条件化并且推断产生观测数据的隐变量的能力。在 Pyro 推断过程中，我们剥离条件化的表达式和其计算, 使得我们能够只写一个随机函数 model 而对许多不同的样本进行条件化. Pyro suppors constraining a model’s internal sample statements to be equal to a given set of observations.

再次考虑称重的例子，也就是 scale. 假设 weight 的分布参数 mu = 8.5, 然后我们得到该物理的一个测量 measurement = 9.5. 那么，需要推断的是 weight 的后验分布:

\[p({\sf weight} \, |{\sf measurement}=9.5 \,; \, \mu=8.5) = \, ?\]

Pyro 用 pyro.condition 来约束 sample statements的取值. pyro.condition 是一个输入是 a model and a dictionary of observations 的高阶函数，它的输出是 a new model that has the same input and output signatures but always uses the given values at observed sample statements:

[5]:

mu = 8.5
conditioned_scale = pyro.condition(scale, data={"measurement": 9.5})
# Input of `pyro.condition`: a model and a dictionary of observations
conditioned_scale(mu)
# Always uses the given values at observed sample statements!

[5]:

9.5

[9]:

import pyro.distributions as dist
from pyro.poutine.trace_messenger import TraceMessenger

cond_data = {"temp": torch.tensor(52)}

with TraceMessenger() as tracer:
    conditioned_scale(mu)

trace = tracer.trace
logp = 0.
for name, node in trace.nodes.items():
    print(name, node['fn'], node['value'], node['is_observed'])
    if node["type"] == "sample":
        logp = logp + node["fn"].log_prob(node["value"]).sum()

weight Normal(loc: 8.5, scale: 1.0) tensor(6.7466) False
measurement Normal(loc: 6.746636867523193, scale: 0.75) 9.5 True

因果它就像常规 Python 函数, conditioning can be deferred or parametrized with Python’s lambda or def:

[4]:

def deferred_conditioned_scale(measurement, mu):
    return pyro.condition(scale, data={"measurement": measurement})(mu)

在某些情况下，直接在 pyro.sample 语句中而不是使用 pyro.condition 定义条件化可能更方便. pyro.sample 的可选参数 obs 就是用于定义条件化:

[5]:

def scale_obs(mu):  # equivalent to conditioned_scale above
    weight = pyro.sample("weight", dist.Normal(mu, 1.))
     # here we condition on measurement == 9.5
    return pyro.sample("measurement", dist.Normal(weight, 0.75), obs=9.5)

最后，除了用于合并观察数据的 pyro.condition 之外，Pyro还包含 pyro.do，这是 Pearl 的 do-operator 的实现，用于因果推断，其接口与 pyro.condition 相同。condition and do 可以自由混合和组合，使Pyro成为基于模型的因果推断的强大工具。

用指导分布近似后验¶

我们可以使用指导函数(guide function)进行灵活的近似推断。

让我们回到 conditioned_scale。现在我们有一个对 measurement 条件化的模型(model)，于是我们可以使用 Pyro 的近似推理算法来估计 weight 已知参数 mu 和给定观测数据 measurement = data 的后验分布.

[14]:

def scale_obs(mu):
    weight = pyro.sample("weight", dist.Normal(mu, 1.))
    return pyro.sample("measurement", dist.Normal(weight, 0.75), obs=9.5)

Pyro中的推理算法，例如 pyro.infer.SVI，允许我们使用任意随机函数，我们将其称为指导函数(guide functions or guides)，作为近似后验分布，指导函数必须满足以下两个条件才能成为特定模型的有效近似后验分布：

所有的非观测变量抽样语句需要在 model 和 guide 中同时出现。
模型分布和指导分布具有相同的输入参数 (input signature).

指导函数的作用(或者角色)是：

作为一个可编程和数据依赖的建议分布(proposal distribution) 用于重要采样, 拒绝采样, 序列蒙特卡罗采样, MCMC, and independent Metropolis-Hastings, and
作为一个变分分布(variational distributions or inference networks) 用于随机变分推理。

目前，重要性抽样，MCMC和随机变分推断已在 Pyro 中实现，我们计划在将来添加其他算法。

尽管指导函数的定义在不同的推断算法中有所不同，但通常应选择 guide function，使其原则上具有足够的灵活性 to closely approximate the distribution over all unobserved samplestatements(也就是非条件化的变量) in the model.

在我们的例子 scale 中, weight 给定参数 mu 和观测 measurement 的真实后验分布是 \(N(9.14, 0.6)\)。 (模型非常简单，因此我们可以解析的得到后验分布, for derivation, see for example Section 3.4 of this book.)

[10]:

def perfect_guide(mu):
    loc =(0.75**2 * mu + 9.5) / (1 + 0.75**2) # 9.14
    scale = np.sqrt(0.75**2/(1 + 0.75**2)) # 0.6
    return pyro.sample("weight", dist.Normal(loc, scale))

[11]:

# Hint for the next section
from torch.distributions import constraints
def scale_parametrized_guide_constrained(mu):
    a = pyro.param("a", torch.tensor(mu))
    b = pyro.param("b", torch.tensor(1.), constraint=constraints.positive)
    return pyro.sample("weight", dist.Normal(a, b))

参数化分布和变分推断¶

Parametrized Stochastic Functions and Variational Inference

尽管我们可以写出 scale 的精确后验分布，但是总的来说，指定一个近似于任意条件随机函数的后验分布的指导分布是很困难的。实际上，可以计算精确后验的随机函数是很少见的。例如，即使在我们的例子 scale 中，如果随机函数的中间过程存在某种非线性，那么可能就是无法计算其精确后验分布:

[16]:

# 随机函数无法计算精确后验分布
def intractable_scale(guess):
    weight = pyro.sample("weight", dist.Normal(guess, 1.0))
    return pyro.sample("measurement", dist.Normal(some_nonlinear_function(weight), 0.75))

因此我们的做法是使用 top-level function pyro.param 来定义一族指导分布 indexed by named parameters, 然后在这族分布中搜索在某种损失意义下最接近真实后验分布的指导分布。这种近似后验推断的方法称为“变分推断”。

pyro.param 是一个 Pyro’s 键值参数存储区(key-value parameter store) 的前端，which is described in more detail in the documentation. 像 pyro.sample 一样，pyro.param 总是以 name 作为第一个参数来调用。 pyro.param 第一次带特定 name 的调用之后, 它把它的参数存储在 parameter store 中, 然后返回该值。之后，当使用该名称进行调用时，它从参数存储区返回值 regardless of any other arguments。这里类似于此处的 simple_param_store.setdefault , 但具有一些附加的跟踪和管理功能。

simple_param_store = {}
a = simple_param_store.setdefault("a", torch.randn(1))

For example, we can parametrize a and b in scale_posterior_guide instead of specifying them by hand:

[8]:

def scale_parametrized_guide(mu):
    a = pyro.param("a", torch.tensor(mu))
    b = pyro.param("b", torch.tensor(1.))
    return pyro.sample("weight", dist.Normal(a, torch.abs(b)))

As an aside, note that in scale_parametrized_guide, we had to apply torch.abs to parameter b 是因为正态分布的标准差必须为正; 类似的约束同样适用于其他许多分布的参数. PyTorch 分布库提供了约束模块(constraints module) 用于实现此类约束, and applying constraints to Pyro parameters is as easy as passing the relevant constraint object to pyro.param:

[9]:

from torch.distributions import constraints

def scale_parametrized_guide_constrained(mu):
    a = pyro.param("a", torch.tensor(mu))
    b = pyro.param("b", torch.tensor(1.), constraint=constraints.positive)
    return pyro.sample("weight", dist.Normal(a, b))  # no more torch.abs

Pyro is built to enable stochastic variational inference, a powerful and widely applicable class of variational inference algorithms with 三个关键特征:

参数都是实数值张量
我们使用模型分布和指导分布的 samples of execution histories 来计算损失函数的蒙特卡罗估计
我们使用随机梯度下降法搜索最佳参数。

将随机梯度下降与 PyTorch 的 GPU 加速张量数学和自动微分相结合，使我们能够在高维参数空间和大规模数据下进行变分推断。

有关 Pyro 的 SVI 功能详细描述参见 SVI tutorial.

例子完整代码¶

我们使用变分推断估计 scale 在已知参数 \(\mu=8.5\)，给定观测 measurement=9.5 之后的后验分布:

[23]:

import matplotlib.pyplot as plt
import numpy as np
import torch

import pyro
import pyro.infer
import pyro.optim
import pyro.distributions as dist
pyro.set_rng_seed(101)
mu = 8.5

def scale(mu):
    weight = pyro.sample("weight", dist.Normal(mu, 1.0))
    return pyro.sample("measurement", dist.Normal(weight, 0.75))
conditioned_scale = pyro.condition(scale, data={"measurement": 9.5})

def scale_parametrized_guide(mu):
    a = pyro.param("a", torch.tensor(mu))
    b = pyro.param("b", torch.tensor(1.))
    return pyro.sample("weight", dist.Normal(a, torch.abs(b)))

pyro.clear_param_store()
svi = pyro.infer.SVI(model=conditioned_scale,
                     guide=scale_parametrized_guide,
                     optim=pyro.optim.SGD({"lr": 0.001, "momentum":0.1}),
                     loss=pyro.infer.Trace_ELBO())

losses, a,b  = [], [], []
num_steps = 2500
for t in range(num_steps):
    losses.append(svi.step(mu))
    a.append(pyro.param("a").item())
    b.append(pyro.param("b").item())

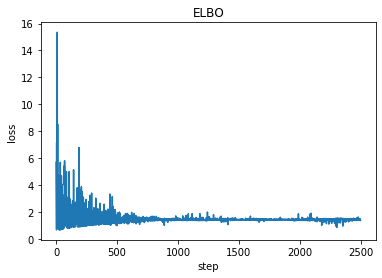
plt.plot(losses)
plt.title("ELBO")
plt.xlabel("step")
plt.ylabel("loss");
print('a = ',pyro.param("a").item())
print('b = ', pyro.param("b").item())

a =  9.107474327087402
b =  0.6285384893417358

[24]:

plt.subplot(1,2,1)
plt.plot([0,num_steps],[9.14,9.14], 'k:')
plt.plot(a)
plt.ylabel('a')

plt.subplot(1,2,2)
plt.ylabel('b')
plt.plot([0,num_steps],[0.6,0.6], 'k:')
plt.plot(b)
plt.tight_layout()

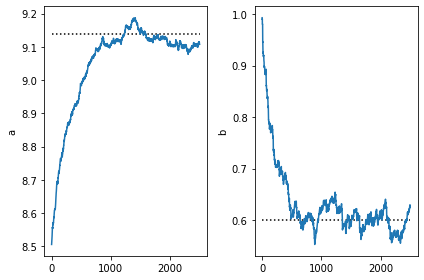
注意，因为我们定义的指导分布和真实后验分布是同一族分布，所以SVI获得的参数非常接近真实参数。

由于优化过程会更新参数存储区中指导分布的参数, 所以一旦我们找到了好的参数, 我们可以将指导分布的样本作为后验样本用于后续任务.

拆解成梯度下降法¶

为了更深一步理解上述的代码，我们把它拆解成梯度下降法。

我们可以用下面代码获得一次执行中涉及的参数。

with pyro.poutine.trace(param_only=True) as param_capture: # 提取参数信息
    loss = loss_fn(conditioned_scale, scale_parametrized_guide, mu)
    loss.backward()
params = [site["value"].unconstrained() for site in param_capture.trace.nodes.values()]

[14]:

import matplotlib.pyplot as plt
import numpy as np
import torch

import pyro
import pyro.infer
import pyro.optim
import pyro.distributions as dist
pyro.set_rng_seed(101)
mu = 8.5

def scale(mu):
    weight = pyro.sample("weight", dist.Normal(mu, 1.0))
    return pyro.sample("measurement", dist.Normal(weight, 0.75))
conditioned_scale = pyro.condition(scale, data={"measurement": torch.tensor(9.5)})

def scale_parametrized_guide(mu):
    a = pyro.param("a", torch.tensor(mu))
    b = pyro.param("b", torch.tensor(1.))
    return pyro.sample("weight", dist.Normal(a, torch.abs(b)))

loss_fn = pyro.infer.Trace_ELBO().differentiable_loss

pyro.clear_param_store()
with pyro.poutine.trace(param_only=True) as param_capture: # 提取参数信息
    loss = loss_fn(conditioned_scale, scale_parametrized_guide, mu)
    loss.backward()
params = [site["value"].unconstrained() for site in param_capture.trace.nodes.values()]

print("Before updated:", pyro.param('a'), pyro.param('b'))

losses, a,b  = [], [], []
lr = 0.001
num_steps = 1000
# 梯度下降参数更新
def step(params):
    for x in params:
        x.data = x.data - lr * x.grad
        x.grad.zero_()

for t in range(num_steps):
    with pyro.poutine.trace(param_only=True) as param_capture:
        loss = loss_fn(conditioned_scale, scale_parametrized_guide, mu)
        loss.backward()
        losses.append(loss.data)

    params = [site["value"].unconstrained() for site in param_capture.trace.nodes.values()]
    a.append(pyro.param("a").item())
    b.append(pyro.param("b").item())
    step(params)
print("After updated:", pyro.param('a'), pyro.param('b'))


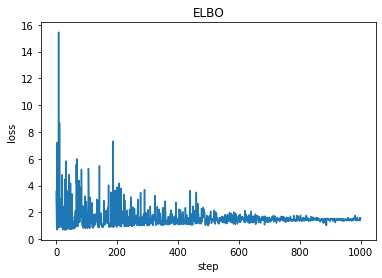
plt.plot(losses)
plt.title("ELBO")
plt.xlabel("step")
plt.ylabel("loss");
print('a = ',pyro.param("a").item())
print('b = ', pyro.param("b").item())

Before updated: tensor(8.5000, requires_grad=True) tensor(1., requires_grad=True)
After updated: tensor(9.0979, requires_grad=True) tensor(0.6203, requires_grad=True)
a =  9.097911834716797
b =  0.6202840209007263

[185]:

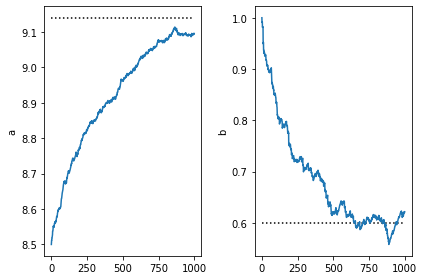
plt.subplot(1,2,1)
plt.plot([0,num_steps],[9.14,9.14], 'k:')
plt.plot(a)
plt.ylabel('a')

plt.subplot(1,2,2)
plt.ylabel('b')
plt.plot([0,num_steps],[0.6,0.6], 'k:')
plt.plot(b)
plt.tight_layout()

下一步？¶

在 Variational Autoencoder tutorial 中，我们将会看到如何使用深度神经网络来增强 scale 这样的模型，以及使用随机变分推断来建立图像生成模型.