Ch15 结果回归模型和倾向得分¶
Outcome Regression and Propensity Scores
内容摘要¶
结果回归和倾向得分分析的各种版本是因果推断最常用的参数方法。您可能想知道为什么我们花这么长时间才包含讨论这些方法的章节。到目前为止,我们已经描述了IP加权,标准化和g估计-g方法。在最不常用的方法之后再提出最常用的方法,对于我们而言似乎是一个奇怪的选择。我们为什么不从基于结果回归和倾向得分的更简单,广泛使用的方法开始呢?因为这些方法通常无法使用。
更准确地说,更简单的结果回归和倾向评分方法(as described in a zillion publications that this chapter cannot possibly summarize)在更简单的环境下可以很好地工作,但这些方法并非handle the complexities associated with causal inference with time-varying treatments. 在第三部分中,我们将再次讨论g方法,但是将不再赘述常规结果回归和倾向评分方法。本章专门讨论因果方法,这些因果方法通常 have limited applicability for complex longitudinal data.
15.1 Outcome regression¶
前面我们介绍了 IP weighting, standardization, and g-estimation to estimate the average causal effect of smoking cessation (the treatment) \(A\) on weight gain (the outcome) \(Y\) . 我们也介绍了如何估计 CATE, either by restricting the analysis to the subset of interest or by adding product terms in marginal structural models (Chapter 12) and structural nested models (Chapter 14).
(G-估计的好处就是避免偏差 induced by misspecifying \(L-Y\) relation) Take structural nested models for example. These models include parameters for the product terms between treatment \(A\) and the variables \(L\), but no parameters for the variables \(L\) themselves. This is an attractive property of structural nested models 是因为我们关注因果效应 of \(A\) on \(Y\) within levels of \(L\) but not in the (noncausal) relation between \(L\) and \(Y\) . A method– g-estimation of structural nested models–that is agnostic about the functional form of the \(L\)-\(Y\) relation is protected from bias due to misspecifying this relation.
如果我们不管偏差 induced by misspecifying \(L-Y\) relation, 那么对应的方法就是 Outcome Regression.
15.2 Propensity scores¶
When using IP weighting (Chapter 12) and g-estimation (Chapter 14), we estimated the probability of treatment given the covariates \(L\), \(P(A = 1|L)\), for each individual. Let us refer to this conditional probability as the propensity score \(\pi(L)\).
15.3 Propensity stratification and standardization¶
The average causal effect among individuals with a particular value \(s\) of the propensity score, i.e.,
under the identifying conditions.
15.4 Propensity matching¶
After propensity matching, the matched population has the \(\pi(L)\) distribution of the treated, of the untreated, or any other arbitrary distribution.
15.5 Propensity models, structural models, predictive models¶
In Part II of this book we have described two different types of models for causal inference: propensity models and structural models. Let us now compare them.
Propensity models are models for the probability of treatment \(A\) given the variables \(L\) used to try to achieve conditional exchangeability. We have used propensity models for matching and stratification in this chapter, for IP weighting in Chapter 12, and for g-estimation in Chapter 14. 倾向模型的参数是 nuisance parameters (see Fine Point 15.1) without a causal interpretation because a variable \(L\) and treatment \(L\) may be associated for many reasons–not only because the variable \(L\) causes \(A\). 倾向模型很有用 as the basis of the estimation of the parameters of structural models, as we have described in this and previous chapters.
Structural models describe the relation between the treatment \(A\) and some component of the distribution (e.g., the mean) of the counterfactual outcome \(Y^a\), either marginally or within levels of the variables \(L\). For continuous treatments, a structural model is often referred to as a dose-response model.
The parameters for treatment in structural models are not nuisance parameters: 他们有直接的因果解释 as outcome differences under different treatment values \(a\).
Programs¶
[1]:
## Setup and imports
%matplotlib inline
import warnings
warnings.filterwarnings('ignore')
import numpy as np
import pandas as pd
import statsmodels.api as sm
import matplotlib.pyplot as plt
from tqdm import tqdm
[4]:
nhefs_all = pd.read_excel('NHEFS.xls')
WARNING *** OLE2 inconsistency: SSCS size is 0 but SSAT size is non-zero
Subset the data as described in the margin, pg 149.
[5]:
restriction_cols = [
'sex', 'age', 'race', 'wt82', 'ht', 'school', 'alcoholpy', 'smokeintensity'
]
missing = nhefs_all[restriction_cols].isnull().any(axis=1)
nhefs = nhefs_all.loc[~missing]
This time, instead of adding dummy variables and squared variables, we’ll use formulas to specify Statsmodels models
Program 15.1¶
“Using the same model as in Section 13.2…”
[6]:
formula = (
'wt82_71 ~ qsmk + qsmk:smokeintensity + sex + race + age + I(age**2) + C(education)'
' + smokeintensity + I(smokeintensity**2) + smokeyrs + I(smokeyrs**2)'
' + C(exercise) + C(active) + wt71 + I(wt71**2)'
)
ols = sm.OLS.from_formula(formula, data=nhefs)
res = ols.fit()
res.summary().tables[1]
[6]:
| coef | std err | t | P>|t| | [0.025 | 0.975] | |
|---|---|---|---|---|---|---|
| Intercept | -1.5882 | 4.313 | -0.368 | 0.713 | -10.048 | 6.872 |
| C(education)[T.2] | 0.7904 | 0.607 | 1.302 | 0.193 | -0.400 | 1.981 |
| C(education)[T.3] | 0.5563 | 0.556 | 1.000 | 0.317 | -0.534 | 1.647 |
| C(education)[T.4] | 1.4916 | 0.832 | 1.792 | 0.073 | -0.141 | 3.124 |
| C(education)[T.5] | -0.1950 | 0.741 | -0.263 | 0.793 | -1.649 | 1.259 |
| C(exercise)[T.1] | 0.2960 | 0.535 | 0.553 | 0.580 | -0.754 | 1.346 |
| C(exercise)[T.2] | 0.3539 | 0.559 | 0.633 | 0.527 | -0.742 | 1.450 |
| C(active)[T.1] | -0.9476 | 0.410 | -2.312 | 0.021 | -1.752 | -0.143 |
| C(active)[T.2] | -0.2614 | 0.685 | -0.382 | 0.703 | -1.604 | 1.081 |
| qsmk | 2.5596 | 0.809 | 3.163 | 0.002 | 0.972 | 4.147 |
| qsmk:smokeintensity | 0.0467 | 0.035 | 1.328 | 0.184 | -0.022 | 0.116 |
| sex | -1.4303 | 0.469 | -3.050 | 0.002 | -2.350 | -0.510 |
| race | 0.5601 | 0.582 | 0.963 | 0.336 | -0.581 | 1.701 |
| age | 0.3596 | 0.163 | 2.202 | 0.028 | 0.039 | 0.680 |
| I(age ** 2) | -0.0061 | 0.002 | -3.534 | 0.000 | -0.009 | -0.003 |
| smokeintensity | 0.0491 | 0.052 | 0.950 | 0.342 | -0.052 | 0.151 |
| I(smokeintensity ** 2) | -0.0010 | 0.001 | -1.056 | 0.291 | -0.003 | 0.001 |
| smokeyrs | 0.1344 | 0.092 | 1.465 | 0.143 | -0.046 | 0.314 |
| I(smokeyrs ** 2) | -0.0019 | 0.002 | -1.209 | 0.227 | -0.005 | 0.001 |
| wt71 | 0.0455 | 0.083 | 0.546 | 0.585 | -0.118 | 0.209 |
| I(wt71 ** 2) | -0.0010 | 0.001 | -1.840 | 0.066 | -0.002 | 6.39e-05 |
[7]:
print(' estimate')
print('alpha_1 {:>6.2f}'.format(res.params.qsmk))
print('alpha_2 {:>6.2f}'.format(res.params['qsmk:smokeintensity']))
estimate
alpha_1 2.56
alpha_2 0.05
To obtain the estimates of the effect of quitting smoking, we’ll use a t_test on the fitted model
First, we’ll construct the a contrast DataFrame for the 5 cigarettes/day example
[8]:
# start with empty DataFrame
contrast = pd.DataFrame(
np.zeros((2, res.params.shape[0])),
columns=res.params.index
)
# modify the entries
contrast['Intercept'] = 1
contrast['qsmk'] = [1, 0]
contrast['smokeintensity'] = [5, 5]
contrast['qsmk:smokeintensity'] = [5, 0]
[9]:
contrast
[9]:
| Intercept | C(education)[T.2] | C(education)[T.3] | C(education)[T.4] | C(education)[T.5] | C(exercise)[T.1] | C(exercise)[T.2] | C(active)[T.1] | C(active)[T.2] | qsmk | ... | sex | race | age | I(age ** 2) | smokeintensity | I(smokeintensity ** 2) | smokeyrs | I(smokeyrs ** 2) | wt71 | I(wt71 ** 2) | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 1 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 1 | ... | 0.0 | 0.0 | 0.0 | 0.0 | 5 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 1 | 1 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0 | ... | 0.0 | 0.0 | 0.0 | 0.0 | 5 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
2 rows × 21 columns
The effect estimate and confidence interval can be calculated with a t-test on row 0 minus row 1
[10]:
res.t_test(contrast.iloc[0] - contrast.iloc[1])
[10]:
<class 'statsmodels.stats.contrast.ContrastResults'>
Test for Constraints
==============================================================================
coef std err t P>|t| [0.025 0.975]
------------------------------------------------------------------------------
c0 2.7929 0.668 4.179 0.000 1.482 4.104
==============================================================================
For the effect estimate with 40 cigarettes/day, we can change a few entries in the contrast DataFrame and again use a t-test
[11]:
contrast['smokeintensity'] = [40, 40]
contrast['qsmk:smokeintensity'] = [40, 0]
res.t_test(contrast.iloc[0] - contrast.iloc[1])
[11]:
<class 'statsmodels.stats.contrast.ContrastResults'>
Test for Constraints
==============================================================================
coef std err t P>|t| [0.025 0.975]
------------------------------------------------------------------------------
c0 4.4261 0.848 5.221 0.000 2.763 6.089
==============================================================================
If we don’t use the product term qsmk:smokeintensity, we get the following model and effect estimate
[12]:
formula = (
'wt82_71 ~ qsmk + sex + race + age + I(age**2) + C(education)'
' + smokeintensity + I(smokeintensity**2) + smokeyrs + I(smokeyrs**2)'
' + C(exercise) + C(active) + wt71 + I(wt71**2)'
) # no qsmk_x_smokeintensity
ols = sm.OLS.from_formula(formula, data=nhefs)
res = ols.fit()
res.summary().tables[1]
[12]:
| coef | std err | t | P>|t| | [0.025 | 0.975] | |
|---|---|---|---|---|---|---|
| Intercept | -1.6586 | 4.314 | -0.384 | 0.701 | -10.120 | 6.803 |
| C(education)[T.2] | 0.8185 | 0.607 | 1.349 | 0.178 | -0.372 | 2.009 |
| C(education)[T.3] | 0.5715 | 0.556 | 1.028 | 0.304 | -0.519 | 1.662 |
| C(education)[T.4] | 1.5085 | 0.832 | 1.812 | 0.070 | -0.124 | 3.141 |
| C(education)[T.5] | -0.1708 | 0.741 | -0.230 | 0.818 | -1.625 | 1.283 |
| C(exercise)[T.1] | 0.3207 | 0.535 | 0.599 | 0.549 | -0.729 | 1.370 |
| C(exercise)[T.2] | 0.3629 | 0.559 | 0.649 | 0.516 | -0.734 | 1.459 |
| C(active)[T.1] | -0.9430 | 0.410 | -2.300 | 0.022 | -1.747 | -0.139 |
| C(active)[T.2] | -0.2580 | 0.685 | -0.377 | 0.706 | -1.601 | 1.085 |
| qsmk | 3.4626 | 0.438 | 7.897 | 0.000 | 2.603 | 4.323 |
| sex | -1.4650 | 0.468 | -3.128 | 0.002 | -2.384 | -0.546 |
| race | 0.5864 | 0.582 | 1.008 | 0.314 | -0.555 | 1.727 |
| age | 0.3627 | 0.163 | 2.220 | 0.027 | 0.042 | 0.683 |
| I(age ** 2) | -0.0061 | 0.002 | -3.555 | 0.000 | -0.010 | -0.003 |
| smokeintensity | 0.0652 | 0.050 | 1.295 | 0.196 | -0.034 | 0.164 |
| I(smokeintensity ** 2) | -0.0010 | 0.001 | -1.117 | 0.264 | -0.003 | 0.001 |
| smokeyrs | 0.1334 | 0.092 | 1.454 | 0.146 | -0.047 | 0.313 |
| I(smokeyrs ** 2) | -0.0018 | 0.002 | -1.183 | 0.237 | -0.005 | 0.001 |
| wt71 | 0.0374 | 0.083 | 0.449 | 0.653 | -0.126 | 0.200 |
| I(wt71 ** 2) | -0.0009 | 0.001 | -1.749 | 0.080 | -0.002 | 0.000 |
[13]:
est = res.params.qsmk
conf_ints = res.conf_int(alpha=0.05, cols=None)
lo, hi = conf_ints[0]['qsmk'], conf_ints[1]['qsmk']
print(' estimate 95% C.I.')
print('alpha_1 {:>5.1f} ({:>0.1f}, {:>0.1f})'.format(est, lo, hi))
estimate 95% C.I.
alpha_1 3.5 (2.6, 4.3)
Program 15.2¶
To estimate propensity score, we fit a logistic model for qsmk conditional on \(L\)
[14]:
formula = (
'qsmk ~ sex + race + age + I(age**2) + C(education)'
' + smokeintensity + I(smokeintensity**2) + smokeyrs + I(smokeyrs**2)'
' + C(exercise) + C(active) + wt71 + I(wt71**2)'
)
model = sm.Logit.from_formula(formula, data=nhefs_all)
res = model.fit(disp=0)
Then propensity is the predicted values
[15]:
propensity = res.predict(nhefs_all)
nhefs_all['propensity'] = propensity
The lowest and highest propensity scores:
[16]:
ranked = nhefs_all[['seqn', 'propensity']].sort_values('propensity').reset_index(drop=True)
[17]:
ranked.loc[0]
[17]:
seqn 22941.000000
propensity 0.052981
Name: 0, dtype: float64
[18]:
ranked.loc[ranked.shape[0] - 1]
[18]:
seqn 24949.000000
propensity 0.793205
Name: 1628, dtype: float64
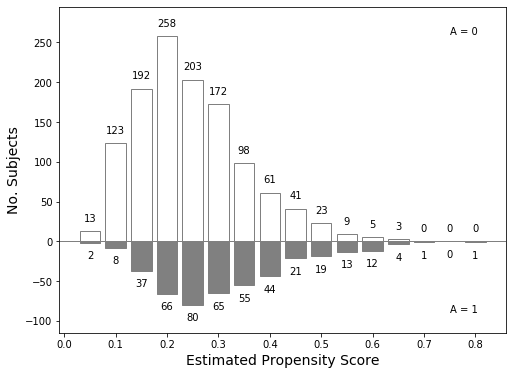
Now we’ll attempt to recreate Figure 15.1, pg 45
First, we’ll split the propensities based on whether the subject quit smoking
[19]:
propensity0 = propensity[nhefs_all.qsmk == 0]
propensity1 = propensity[nhefs_all.qsmk == 1]
It looks like the bins are spaced every 0.05 (except at the right end), with the first bin starting at 0.025.
[20]:
bins = np.arange(0.025, 0.85, 0.05)
top0, _ = np.histogram(propensity0, bins=bins)
top1, _ = np.histogram(propensity1, bins=bins)
[21]:
fig, ax = plt.subplots(figsize=(8, 6))
ax.set_ylim(-115, 295)
ax.axhline(0, c='gray', linewidth=1)
bars0 = ax.bar(bins[:-1] + 0.025, top0, width=0.04, facecolor='white')
bars1 = ax.bar(bins[:-1] + 0.025, -top1, width=0.04, facecolor='gray')
for bars in (bars0, bars1):
for bar in bars:
bar.set_edgecolor("gray")
for x, y in zip(bins, top0):
ax.text(x + 0.025, y + 10, str(y), ha='center', va='bottom')
for x, y in zip(bins, top1):
ax.text(x + 0.025, -y - 10, str(y), ha='center', va='top')
ax.text(0.75, 260, "A = 0")
ax.text(0.75, -90, "A = 1")
ax.set_ylabel("No. Subjects", fontsize=14)
ax.set_xlabel("Estimated Propensity Score", fontsize=14);
[22]:
print(' mean propensity')
print(' non-quitters: {:>0.3f}'.format(propensity0.mean()))
print(' quitters: {:>0.3f}'.format(propensity1.mean()))
mean propensity
non-quitters: 0.245
quitters: 0.312
Program 15.3¶
“only individual 22005 had an estimated \(\pi(L)\) of 0.6563”, pg 186
[23]:
nhefs_all[['seqn', 'propensity']].loc[abs(propensity - 0.6563) < 1e-4]
[23]:
| seqn | propensity | |
|---|---|---|
| 1088 | 22005 | 0.656281 |
Create the deciles and check their counts
[24]:
nhefs_all['decile'] = pd.qcut(nhefs_all.propensity, 10, labels=list(range(10)))
[25]:
nhefs_all.decile.value_counts(sort=False)
[25]:
0 163
1 163
2 163
3 163
4 163
5 162
6 163
7 163
8 163
9 163
Name: decile, dtype: int64
Now create a model with interaction between qsmk and \(L\)
[26]:
model = sm.OLS.from_formula(
'wt82_71 ~ qsmk*C(decile)',
data=nhefs_all
)
res = model.fit()
[27]:
res.summary().tables[1]
[27]:
| coef | std err | t | P>|t| | [0.025 | 0.975] | |
|---|---|---|---|---|---|---|
| Intercept | 3.9952 | 0.630 | 6.338 | 0.000 | 2.759 | 5.232 |
| C(decile)[T.1] | -1.0905 | 0.916 | -1.190 | 0.234 | -2.888 | 0.707 |
| C(decile)[T.2] | -1.3831 | 0.918 | -1.506 | 0.132 | -3.184 | 0.418 |
| C(decile)[T.3] | -0.5205 | 0.926 | -0.562 | 0.574 | -2.337 | 1.295 |
| C(decile)[T.4] | -1.8964 | 0.940 | -2.017 | 0.044 | -3.741 | -0.052 |
| C(decile)[T.5] | -2.1482 | 0.954 | -2.252 | 0.024 | -4.019 | -0.277 |
| C(decile)[T.6] | -2.4352 | 0.949 | -2.566 | 0.010 | -4.297 | -0.574 |
| C(decile)[T.7] | -3.7105 | 0.974 | -3.810 | 0.000 | -5.621 | -1.800 |
| C(decile)[T.8] | -4.8907 | 1.034 | -4.731 | 0.000 | -6.918 | -2.863 |
| C(decile)[T.9] | -4.4996 | 1.049 | -4.288 | 0.000 | -6.558 | -2.441 |
| qsmk | -0.0147 | 2.389 | -0.006 | 0.995 | -4.700 | 4.671 |
| qsmk:C(decile)[T.1] | 4.1634 | 2.897 | 1.437 | 0.151 | -1.520 | 9.847 |
| qsmk:C(decile)[T.2] | 6.5591 | 2.884 | 2.275 | 0.023 | 0.903 | 12.215 |
| qsmk:C(decile)[T.3] | 2.3570 | 2.808 | 0.839 | 0.401 | -3.151 | 7.865 |
| qsmk:C(decile)[T.4] | 4.1450 | 2.754 | 1.505 | 0.132 | -1.257 | 9.547 |
| qsmk:C(decile)[T.5] | 4.5580 | 2.759 | 1.652 | 0.099 | -0.853 | 9.969 |
| qsmk:C(decile)[T.6] | 4.3306 | 2.776 | 1.560 | 0.119 | -1.115 | 9.776 |
| qsmk:C(decile)[T.7] | 3.5847 | 2.744 | 1.307 | 0.192 | -1.797 | 8.966 |
| qsmk:C(decile)[T.8] | 2.3155 | 2.700 | 0.858 | 0.391 | -2.981 | 7.612 |
| qsmk:C(decile)[T.9] | 2.2549 | 2.687 | 0.839 | 0.402 | -3.016 | 7.526 |
To get the effect estimates, we’ll use t-tests with contrast DataFrames, like we did in Program 15.1
[28]:
# start with empty DataFrame
contrast = pd.DataFrame(
np.zeros((2, res.params.shape[0])),
columns=res.params.index
)
# modify the constant entries
contrast['Intercept'] = 1
contrast['qsmk'] = [1, 0]
# loop through t-tests, modify the DataFrame for each decile,
# and print out effect estimate and confidence intervals
print(' estimate 95% C.I.\n')
for i in range(10):
if i != 0:
# set the decile number
contrast['C(decile)[T.{}]'.format(i)] = [1, 1]
contrast['qsmk:C(decile)[T.{}]'.format(i)] = [1, 0]
ttest = res.t_test(contrast.iloc[0] - contrast.iloc[1])
est = ttest.effect[0]
conf_ints = ttest.conf_int(alpha=0.05)
lo, hi = conf_ints[0, 0], conf_ints[0, 1]
print('decile {} {:>5.1f} ({:>4.1f},{:>4.1f})'.format(i, est, lo, hi))
if i != 0:
# reset to zero
contrast['C(decile)[T.{}]'.format(i)] = [0, 0]
contrast['qsmk:C(decile)[T.{}]'.format(i)] = [0, 0]
estimate 95% C.I.
decile 0 -0.0 (-4.7, 4.7)
decile 1 4.1 ( 0.9, 7.4)
decile 2 6.5 ( 3.4, 9.7)
decile 3 2.3 (-0.6, 5.2)
decile 4 4.1 ( 1.4, 6.8)
decile 5 4.5 ( 1.8, 7.2)
decile 6 4.3 ( 1.5, 7.1)
decile 7 3.6 ( 0.9, 6.2)
decile 8 2.3 (-0.2, 4.8)
decile 9 2.2 (-0.2, 4.7)
We can compare the estimates above to the estimate we get from a model without interaction between qsmk and \(L\)
[29]:
model = sm.OLS.from_formula(
'wt82_71 ~ qsmk + C(decile)',
data=nhefs_all
)
res = model.fit()
[30]:
res.summary().tables[1]
[30]:
| coef | std err | t | P>|t| | [0.025 | 0.975] | |
|---|---|---|---|---|---|---|
| Intercept | 3.7505 | 0.609 | 6.159 | 0.000 | 2.556 | 4.945 |
| C(decile)[T.1] | -0.7391 | 0.861 | -0.858 | 0.391 | -2.428 | 0.950 |
| C(decile)[T.2] | -0.6182 | 0.861 | -0.718 | 0.473 | -2.307 | 1.071 |
| C(decile)[T.3] | -0.5204 | 0.858 | -0.606 | 0.544 | -2.204 | 1.163 |
| C(decile)[T.4] | -1.4884 | 0.859 | -1.733 | 0.083 | -3.173 | 0.197 |
| C(decile)[T.5] | -1.6227 | 0.868 | -1.871 | 0.062 | -3.324 | 0.079 |
| C(decile)[T.6] | -1.9853 | 0.868 | -2.287 | 0.022 | -3.688 | -0.282 |
| C(decile)[T.7] | -3.4447 | 0.875 | -3.937 | 0.000 | -5.161 | -1.729 |
| C(decile)[T.8] | -5.1544 | 0.885 | -5.825 | 0.000 | -6.890 | -3.419 |
| C(decile)[T.9] | -4.8403 | 0.883 | -5.483 | 0.000 | -6.572 | -3.109 |
| qsmk | 3.5005 | 0.457 | 7.659 | 0.000 | 2.604 | 4.397 |
[31]:
est = res.params.qsmk
conf_ints = res.conf_int(alpha=0.05, cols=None)
lo, hi = conf_ints[0]['qsmk'], conf_ints[1]['qsmk']
print(' estimate 95% C.I.')
print('effect {:>5.1f} ({:>0.1f}, {:>0.1f})'.format(est, lo, hi))
estimate 95% C.I.
effect 3.5 (2.6, 4.4)
Program 15.4¶
Now we will do “outcome regression \(\mathrm{E}[Y|A, C=0, p(L)]\) with the estimated propensity score \(p(L)\) as a continuous covariate rather than as a set of indicators” (pg 187)
[32]:
nhefs['propensity'] = propensity[~nhefs_all.wt82_71.isnull()]
[33]:
model = sm.OLS.from_formula('wt82_71 ~ qsmk + propensity', data=nhefs)
res = model.fit()
res.summary().tables[1]
[33]:
| coef | std err | t | P>|t| | [0.025 | 0.975] | |
|---|---|---|---|---|---|---|
| Intercept | 5.5945 | 0.483 | 11.581 | 0.000 | 4.647 | 6.542 |
| qsmk | 3.5506 | 0.457 | 7.765 | 0.000 | 2.654 | 4.448 |
| propensity | -14.8218 | 1.758 | -8.433 | 0.000 | -18.269 | -11.374 |
From the coefficient on qsmk we can see the effect estimate is 3.6.
We’ll use bootstrap to get confidence intervals.
[34]:
def outcome_regress_effect(data):
model = sm.OLS.from_formula('wt82_71 ~ qsmk + propensity', data=data)
res = model.fit()
data_qsmk_1 = data.copy()
data_qsmk_1['qsmk'] = 1
data_qsmk_0 = data.copy()
data_qsmk_0['qsmk'] = 0
mean_qsmk_1 = res.predict(data_qsmk_1).mean()
mean_qsmk_0 = res.predict(data_qsmk_0).mean()
return mean_qsmk_1 - mean_qsmk_0
[35]:
def nonparametric_bootstrap(data, func, n=1000):
estimate = func(data)
n_rows = data.shape[0]
indices = list(range(n_rows))
b_values = []
for _ in tqdm(range(n)):
data_b = data.sample(n=n_rows, replace=True)
b_values.append(func(data_b))
std = np.std(b_values)
return estimate, (estimate - 1.96 * std, estimate + 1.96 * std)
[36]:
data = nhefs[['wt82_71', 'qsmk', 'propensity']]
info = nonparametric_bootstrap(
data, outcome_regress_effect, n=2000
)
100%|██████████| 2000/2000 [00:29<00:00, 67.98it/s]
[37]:
print(' estimate 95% C.I.')
print('effect {:>5.1f} ({:>0.1f}, {:>0.1f})'.format(info[0], info[1][0], info[1][1]))
estimate 95% C.I.
effect 3.6 (2.6, 4.5)
用类组织本章的代码¶
结果回归和倾向得分分析的各种版本是因果推断最常用的参数方法。那么本类主要目的是用于展示这两种因果效应估计方法的实现。
[1]:
%matplotlib inline
import warnings
warnings.filterwarnings('ignore')
import numpy as np
import pandas as pd
import statsmodels.api as sm
import matplotlib.pyplot as plt
from tqdm import tqdm
[91]:
class CH15(object):
def __init__(self):
print('这是一个结果回归和倾向得分因果效应估计方法的展示类!')
self.data = self.get_data()
def get_data(self):
nhefs_all = pd.read_excel('NHEFS.xls')
restriction_cols = [
'sex', 'age', 'race', 'wt82', 'ht', 'school', 'alcoholpy', 'smokeintensity'
]
missing = nhefs_all[restriction_cols].isnull().any(axis=1)
nhefs = nhefs_all.loc[~missing]
print("我们的展示数据是 NHEFS with shape", nhefs.shape)
return nhefs
def outcome_regression(self):
formula = (
'wt82_71 ~ qsmk + qsmk:smokeintensity + sex + race + age + I(age**2) + C(education)'
' + smokeintensity + I(smokeintensity**2) + smokeyrs + I(smokeyrs**2)'
' + C(exercise) + C(active) + wt71 + I(wt71**2)'
)
ols = sm.OLS.from_formula(formula, data=self.data)
res = ols.fit()
print(' estimate')
print('alpha_1 {:>6.2f}'.format(res.params.qsmk))
print('alpha_2 {:>6.2f}'.format(res.params['qsmk:smokeintensity']))
est = res.params.qsmk
conf_ints = res.conf_int(alpha=0.05, cols=None)
lo, hi = conf_ints[0]['qsmk'], conf_ints[1]['qsmk']
print(' estimate 95% C.I.')
print('alpha_1 {:>5.2f} ({:>0.2f}, {:>0.2f})'.format(est, lo, hi))
return res.summary().tables[1]
def ps_score(self):
nhefs_all = pd.read_excel('NHEFS.xls')
formula = (
'qsmk ~ sex + race + age + I(age**2) + C(education)'
' + smokeintensity + I(smokeintensity**2) + smokeyrs + I(smokeyrs**2)'
' + C(exercise) + C(active) + wt71 + I(wt71**2)'
)
model = sm.Logit.from_formula(formula, data=nhefs_all)
res = model.fit(disp=0)
propensity = res.predict(nhefs_all)
propensity0 = propensity[nhefs_all.qsmk == 0]
propensity1 = propensity[nhefs_all.qsmk == 1]
bins = np.arange(0.025, 0.85, 0.05)
top0, _ = np.histogram(propensity0, bins=bins)
top1, _ = np.histogram(propensity1, bins=bins)
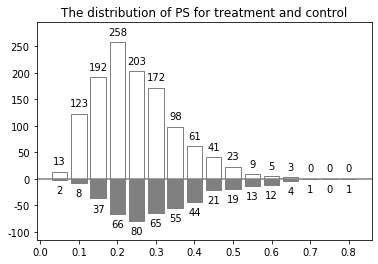
plt.ylim(-115, 295)
plt.axhline(0, c='gray')
plt.title("The distribution of PS for treatment and control")
bars0 = plt.bar(bins[:-1] + 0.025, top0, width=0.04, facecolor='white')
bars1 = plt.bar(bins[:-1] + 0.025, -top1, width=0.04, facecolor='gray')
for bars in (bars0, bars1):
for bar in bars:
bar.set_edgecolor("gray")
for x, y in zip(bins, top0):
plt.text(x + 0.025, y + 10, str(y), ha='center', va='bottom')
for x, y in zip(bins, top1):
plt.text(x + 0.025, -y - 10, str(y), ha='center', va='top')
print(' mean propensity')
print(' non-quitters: {:>0.3f}'.format(propensity0.mean()))
print(' quitters: {:>0.3f}'.format(propensity1.mean()))
print()
return propensity
def ps_stratification_standardization(self):
dat = self.data
propensity = self.ps_score()
dat['propensity'] = propensity
dat['decile'] = pd.qcut(dat.propensity, 10, labels=list(range(10)))
model = sm.OLS.from_formula(
'wt82_71 ~ qsmk + C(decile)',
data=dat
)
res = model.fit()
est = res.params.qsmk
conf_ints = res.conf_int(alpha=0.05, cols=None)
lo, hi = conf_ints[0]['qsmk'], conf_ints[1]['qsmk']
print(' estimate 95% C.I.')
print('effect {:>5.1f} ({:>0.1f}, {:>0.1f})'.format(est, lo, hi))
return est
def ps_outcome_regression(self):
nhefs = self.data
propensity = self.ps_score()
nhefs['propensity'] = propensity
def outcome_regress_effect(data):
model = sm.OLS.from_formula('wt82_71 ~ qsmk + propensity', data=data)
res = model.fit()
data_qsmk_1 = data.copy()
data_qsmk_1['qsmk'] = 1
data_qsmk_0 = data.copy()
data_qsmk_0['qsmk'] = 0
mean_qsmk_1 = res.predict(data_qsmk_1).mean()
mean_qsmk_0 = res.predict(data_qsmk_0).mean()
return mean_qsmk_1 - mean_qsmk_0
# 通过重新采样狗仔置信区间
def nonparametric_bootstrap(data, func, n=1000):
estimate = func(data)
n_rows = data.shape[0]
indices = list(range(n_rows))
b_values = []
for _ in tqdm(range(n)):
data_b = data.sample(n=n_rows, replace=True)
b_values.append(func(data_b))
std = np.std(b_values)
return estimate, (estimate - 1.96 * std, estimate + 1.96 * std)
data = nhefs[['wt82_71', 'qsmk', 'propensity']]
info = nonparametric_bootstrap(
nhefs, outcome_regress_effect, n=200
)
print(' estimate 95% C.I.')
print('effect {:>5.1f} ({:>0.1f}, {:>0.1f})'.format(info[0], info[1][0], info[1][1]))
return info[0]
g = CH15()
# g.ps_stratification_standardization()
g.ps_outcome_regression()
这是一个结果回归和倾向得分因果效应估计方法的展示类!
WARNING *** OLE2 inconsistency: SSCS size is 0 but SSAT size is non-zero
我们的展示数据是 NHEFS with shape (1566, 64)
WARNING *** OLE2 inconsistency: SSCS size is 0 but SSAT size is non-zero
2%|▏ | 4/200 [00:00<00:05, 33.17it/s]
mean propensity
non-quitters: 0.245
quitters: 0.312
100%|██████████| 200/200 [00:05<00:00, 33.52it/s]
estimate 95% C.I.
effect 3.6 (2.6, 4.5)
[91]:
3.550595680031253
[ ]: